Pisagor Teoremi (Bağıntısı) Nedir?

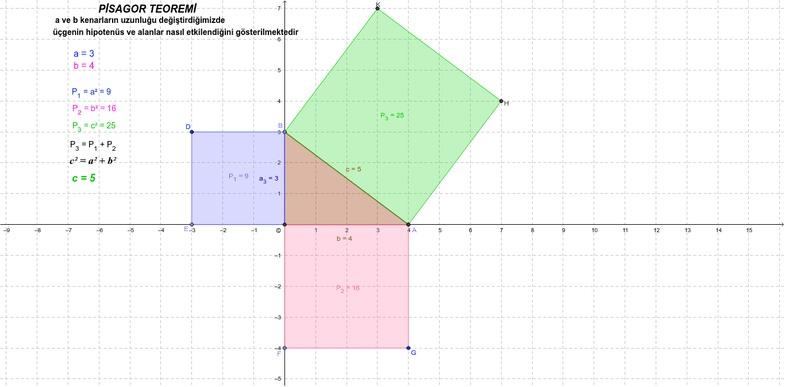
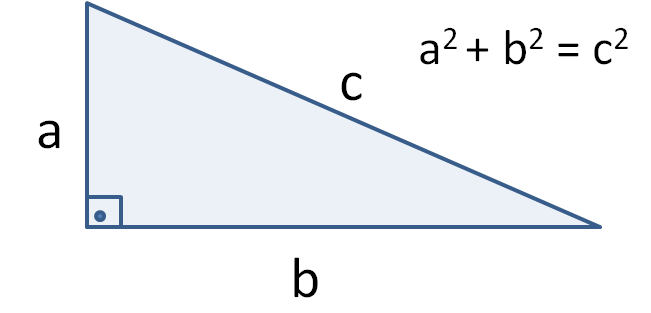
Matematikle doğrudan ilişkili olan Pisagor teoremi, adını bu teoremi keşfeden Pisagor’dan almaktadır. Bu teorem, dik üçgenlerin kenarları arasındaki özel bir ilişkiyi açıklar. Bir dik açının karşısındaki kenar hipotenüs olarak bilinir ve bu teoreme göre hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir. Temel bir matematik ilkesi olan Pisagor teoremini şu basit formülle ifade edebiliriz: a2+b2=c2
burada a, b ve c üçgenin kenarlarını temsil eder. Bu formül, üçgenin dik kenarlarıyla birlikte hipotenüsün değerini hesaplamamıza olanak tanır. Pisagor teoremi, aynı zamanda Pisagor denklemi veya Pisagor bağıntısı olarak da bilinir. Bu matematiksel ilke, geometri ve trigonometri alanlarında temel bir taşıyıcı olarak önemli bir yer tutar.
Pisagor teoremi sadece üçgen kenarlarını değil, aynı zamanda üçgenin açılarını da bulma imkanı sunar. Örneğin, bir üçgen ikizkenarsa, iki kenar açısı da 45 derecedir. Bu nedenle Pisagor teoreminin sabit formülünü iyi anlamak ve akılda tutmak önemlidir. Bu sayede öğrenciler, işlem sırasında daha fazla kolaylık elde edebilirler.
Pisagor teoremi, matematiksel temsilini a2+b2=c2 formülüyle taşır ve bu formül, üçgenin kenarları arasındaki ilişkiyi anlamak adına temel bir araçtır. Bu matematik ilkesi, hem kenarları hem de açıları keşfetme konusunda öğrencilere kapsamlı bir kılavuz sunar, böylece matematikle ilgili kavramları daha etkili bir şekilde öğrenirler.
Pisagor Teoreminin Kanıtları Nelerdir?
Pisagor teoremi, diğer matematiksel teoremler gibi kanıtlara dayanır. Her bir kanıt, teoremin doğruluğunu göstermenin yanı sıra uygulanamayacağı koşulları da açıklamayı amaçlar. Pisagor teoremi, matematik tarihinde en eski ve hala kullanılan teorilerden biridir ve bu nedenle defalarca kanıtlanmıştır. Öklid ve Bhaskara gibi birçok kanıta dayanarak Pisagor teoreminden yola çıkabiliriz. Bu kanıtlar, teoremin evrensel doğruluğunu ortaya koymak için önemli bir rol oynamaktadır.
Öklid’in ispatına göre, öncelikle dik bir A B C üçgeni çizilir. Burada A açısı dik olacak şekilde yer alır. Daha sonra, üçgenin kenar uzunluğunu A B C üçgeninin kenar uzunluğu olacak şekilde etrafına kareler çizilir. A noktasından başlayarak, D ve E kenarlarına doğru birer dik çizilir. Öklid’in ispatına göre, çizilen dik şeklin iki tarafındaki alanlar eşit olduğu bulunur. İki küçük karenin alanı, hipotenüsün karesi alanına eşittir.
Bhaskara’nın ispatına göre ise, öncelikle bir dik üçgen çizilir ve hipotenüse bir dik çizilir. Bu durumda, üçgen benzerlik kurallarını göz önünde bulundurarak A B C üçgeni ile C B E üçgeninin benzer olduğu görülür. Bu, B açısının ortak bir açı olmasından kaynaklanır. E ve C açıları da her iki üçgenin de dik açıları olarak kabul edilir. Bu şekilde Bhaskara ispatı, Pisagor teoremini doğrulamak için kullanılır.
Pisagor Teoreminin Günlük Hayatta Kullanım Alanları Nelerdir?
Pisagor teoreminin matematikteki kilit rolünü vurguladık. Fakat aynı zamanda günlük hayatta birçok alanda nasıl kullanıldığına da değinmek önemlidir. İnşaattan navigasyona kadar çeşitli sektörlerde Pisagor teoremi etkin bir şekilde kullanılmaktadır. Örneğin, standart tekniklerle ölçülemeyen dağ ve tepe yüksekliklerini belirlemek için Pisagor teoremi kullanılır.
Daha detaylı bir bakış açısıyla, inşaat ve mimarlık alanlarında bu teorem oldukça önemlidir. Pisagor teoremine göre çizilen düz iki çizgi arasındaki diyagonalin uzunluğu hesaplanarak, mimari ve inşaat projelerinde kullanılabilecek bilgiler elde edilir. Bu uygulama genellikle mimari tasarımların yanı sıra ahşap işlerinde de pratik bir şekilde kullanılır.
Navigasyon bağlamında, Pisagor teoremi en kısa mesafeyi bulma konusunda yol gösterici olarak işlev görür. Örneğin, bir uçağın yerden yüksekliği ve hedef iniş noktasından uzaklığındaki açılar, doğru iniş noktasını belirlemek için kullanılabilir. Pisagor teoremi, farklı alanlarda pratik ve etkili bir araç olarak geniş bir uygulama yelpazesi sunmaktadır.
Pisagor Teoremi İle İlgili Videolar